Chasse Deau Equation
Chasse deau equation – L’équation de chasse d’eau est un outil essentiel pour comprendre et analyser le fonctionnement des systèmes d’évacuation. Elle permet de prédire le débit d’eau, le temps de vidange et les dimensions optimales des tuyaux, en tenant compte de facteurs clés comme la pression d’alimentation, la géométrie du tuyau et la viscosité du fluide.
En utilisant des principes physiques tels que la conservation de la masse et de l’énergie, l’équation de chasse d’eau permet de modéliser le mouvement de l’eau dans les systèmes d’évacuation. Elle trouve des applications dans la conception de systèmes d’évacuation efficaces, l’analyse des performances existantes et la prédiction du temps de vidange.
Introduction à l’équation de chasse d’eau
L’équation de chasse d’eau est un outil essentiel pour comprendre et analyser le comportement des systèmes d’évacuation, notamment les systèmes de drainage, les égouts et les conduites d’eau. Cette équation permet de prédire le temps de vidange d’un réservoir ou d’un tuyau, en tenant compte de différents facteurs tels que le débit, la hauteur de chute et la section transversale du tuyau.
L’équation de chasse d’eau est basée sur le principe de conservation de la masse et de l’énergie, et elle prend en compte la vitesse de l’eau, la gravité et les pertes de charge dues au frottement dans le tuyau. Elle permet de déterminer la vitesse et le débit de l’eau dans le système d’évacuation, ce qui est crucial pour assurer un fonctionnement optimal et éviter les problèmes de débordement ou de stagnation.
Variables clés de l’équation de chasse d’eau
Les variables clés qui influencent l’équation de chasse d’eau sont :
- Débit (Q): Le débit représente la quantité d’eau qui s’écoule à travers une section donnée du tuyau par unité de temps. Il est généralement mesuré en mètres cubes par seconde (m³/s) ou en litres par seconde (l/s).
- Hauteur de chute (H): La hauteur de chute correspond à la différence de niveau entre le point d’entrée et le point de sortie du tuyau. Elle est mesurée en mètres (m).
- Section transversale du tuyau (A): La section transversale du tuyau représente la surface de la section transversale du tuyau, mesurée en mètres carrés (m²).
Applications de l’équation de chasse d’eau
L’équation de chasse d’eau trouve des applications dans plusieurs domaines liés à la conception et à l’analyse des systèmes d’évacuation :
- Conception des systèmes d’évacuation: L’équation de chasse d’eau permet de déterminer la taille optimale des tuyaux et des réservoirs pour assurer un écoulement efficace de l’eau et éviter les problèmes de débordement ou de stagnation.
- Analyse des performances: L’équation de chasse d’eau peut être utilisée pour analyser les performances des systèmes d’évacuation existants, en déterminant le temps de vidange, la vitesse de l’eau et les pertes de charge.
- Prédiction du temps de vidange: L’équation de chasse d’eau permet de prédire le temps de vidange d’un réservoir ou d’un tuyau, en fonction du débit, de la hauteur de chute et de la section transversale du tuyau.
Dérivation de l’équation de chasse d’eau
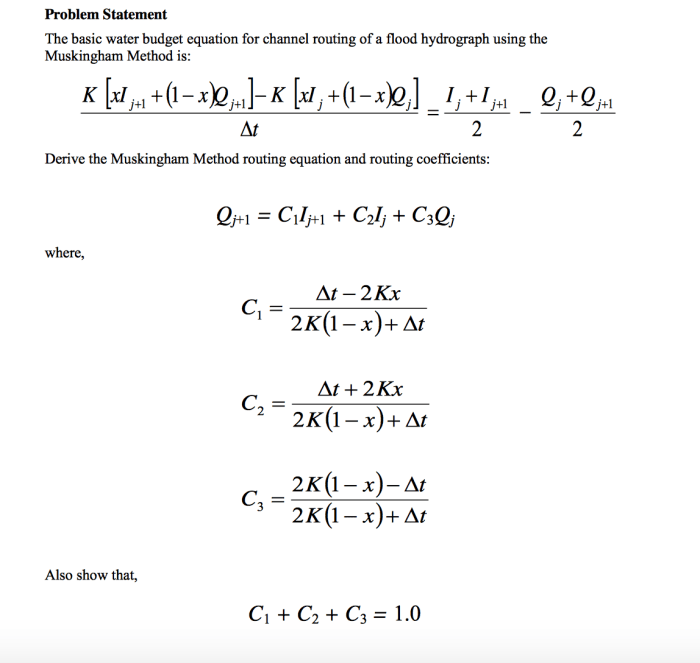
La dérivation de l’équation de chasse d’eau repose sur des principes physiques fondamentaux, tels que la conservation de la masse et de l’énergie. Cette équation permet de modéliser le comportement du flux d’eau dans un système de chasse d’eau, ce qui est crucial pour la conception et l’optimisation de ces systèmes.
Principes physiques
La conservation de la masse et de l’énergie sont les deux principes fondamentaux qui sous-tendent la dérivation de l’équation de chasse d’eau. La conservation de la masse stipule que la masse totale d’un système reste constante, même si elle peut changer de forme ou d’état.
En d’autres termes, la masse ne peut être ni créée ni détruite, mais elle peut être transformée d’une forme à une autre. La conservation de l’énergie stipule que l’énergie totale d’un système reste constante, même si elle peut être transformée d’une forme à une autre.
En d’autres termes, l’énergie ne peut être ni créée ni détruite, mais elle peut être transférée d’un système à un autre ou transformée d’une forme à une autre.
Étapes de la dérivation, Chasse deau equation
La dérivation de l’équation de chasse d’eau implique les étapes suivantes :
- Définir les variables clés du système, telles que le débit d’eau, la hauteur de la colonne d’eau, la pression, etc.
- Appliquer le principe de conservation de la masse pour établir une relation entre le débit d’eau et la vitesse de l’eau dans le système.
- Appliquer le principe de conservation de l’énergie pour établir une relation entre la pression, la hauteur de la colonne d’eau et la vitesse de l’eau.
- Combiner les équations de conservation de la masse et de l’énergie pour obtenir l’équation de chasse d’eau.
Application de l’équation de chasse d’eau
L’équation de chasse d’eau peut être appliquée à divers systèmes d’évacuation, tels que les toilettes, les douches, les lavabos et les éviers. Elle permet de déterminer les paramètres clés du système, tels que le temps de vidange, le débit d’eau et la hauteur de la colonne d’eau.
Par exemple, l’équation de chasse d’eau peut être utilisée pour calculer le temps de vidange d’une toilette. En connaissant le volume de la cuvette et le débit d’eau, l’équation peut être utilisée pour déterminer le temps nécessaire pour vider complètement la cuvette.
De plus, l’équation de chasse d’eau peut être utilisée pour optimiser la conception des systèmes d’évacuation. En ajustant les paramètres du système, tels que la taille du tuyau et la hauteur de la colonne d’eau, il est possible de minimiser le temps de vidange et de maximiser l’efficacité du système.
Facteurs influençant la chasse d’eau
L’équation de chasse d’eau, que nous avons dérivée précédemment, est un outil précieux pour comprendre le comportement d’un réservoir se vidant. Cependant, il est important de noter que cette équation est basée sur un certain nombre d’hypothèses simplificatrices. En réalité, de nombreux facteurs peuvent influencer le débit de la chasse d’eau, affectant ainsi la précision des prédictions faites à partir de l’équation.
Dans cette section, nous allons explorer certains de ces facteurs importants et analyser leur impact sur la vitesse d’écoulement, la hauteur de chute et le temps de vidange.
Pression d’alimentation
La pression d’alimentation est l’un des facteurs les plus importants qui influencent le débit de la chasse d’eau. Une pression d’alimentation plus élevée entraîne un débit plus important, car la force qui pousse l’eau à travers le tuyau est plus grande.
La vitesse d’écoulement est directement proportionnelle à la racine carrée de la pression d’alimentation.
Par exemple, si la pression d’alimentation est doublée, la vitesse d’écoulement augmentera d’un facteur √2, soit environ 1,41. Cela signifie que l’eau s’écoulera plus rapidement et que le réservoir se videra plus rapidement.
Géométrie du tuyau
La géométrie du tuyau, y compris son diamètre et sa longueur, a un impact significatif sur le débit de la chasse d’eau. Un tuyau plus large permet à l’eau de s’écouler plus facilement, tandis qu’un tuyau plus long augmente la résistance à l’écoulement.
The Chassée d’Eau equation is a fascinating mathematical tool used to analyze the flow of water through complex systems. It’s a powerful tool, just like the ingenuity required to repurpose old pallets into a sturdy bed frame. If you’re interested in learning more about this creative DIY project, you can find some helpful tips and instructions on faire un sommier avec des palettes.
While this project might not directly relate to the Chassée d’Eau equation, it demonstrates the same kind of resourcefulness and problem-solving that drives innovation in all fields.
Le débit est inversement proportionnel à la longueur du tuyau et proportionnel au carré du diamètre du tuyau.
Par exemple, si le diamètre du tuyau est doublé, le débit augmentera d’un facteur 4. Inversement, si la longueur du tuyau est doublée, le débit sera réduit de moitié.
Viscosité du fluide
La viscosité du fluide, qui est une mesure de sa résistance à l’écoulement, peut également influencer le débit de la chasse d’eau. Une viscosité plus élevée signifie que l’eau s’écoulera plus lentement.
La vitesse d’écoulement est inversement proportionnelle à la viscosité du fluide.
Par exemple, si la viscosité de l’eau est doublée, la vitesse d’écoulement sera réduite de moitié.
Applications de l’équation de chasse d’eau
L’équation de chasse d’eau, aussi connue sous le nom d’équation de Bernoulli, est un outil précieux pour la conception et l’analyse des systèmes d’évacuation. Elle permet de prédire le comportement du fluide dans les tuyaux et de calculer des paramètres clés comme le débit, le temps de vidange et les dimensions optimales des conduits.
Exemples d’applications de l’équation de chasse d’eau
Voici quelques exemples concrets de l’utilisation de l’équation de chasse d’eau dans la pratique :
| Description | Application | Équation utilisée | Résultats |
|---|---|---|---|
| Calcul du débit de la chasse d’eau d’une toilette | Déterminer le volume d’eau nécessaire pour évacuer les déchets |
Où : Q = Débit (m 3/s) A = Aire de la section transversale du tuyau (m 2) V = Vitesse du fluide (m/s) |
Le débit de la chasse d’eau est généralement compris entre 6 et 12 litres par minute. |
| Calcul du temps de vidange d’un réservoir | Déterminer le temps nécessaire pour vider complètement un réservoir d’eau |
Où : t = Temps de vidange (s) V = Volume du réservoir (m 3) Q = Débit de la chasse d’eau (m 3/s) |
Le temps de vidange d’un réservoir dépend du volume du réservoir et du débit de la chasse d’eau. |
| Calcul des dimensions des tuyaux | Déterminer le diamètre optimal des tuyaux pour assurer un écoulement efficace |
Où : Q = Débit (m 3/s) D = Diamètre du tuyau (m) V = Vitesse du fluide (m/s) |
Les dimensions des tuyaux doivent être choisies en fonction du débit de la chasse d’eau et de la vitesse du fluide pour éviter les pertes de charge et les problèmes de drainage. |
Limitations de l’équation de chasse d’eau
L’équation de chasse d’eau, bien qu’utile pour modéliser le comportement des systèmes d’évacuation, présente certaines limitations qui doivent être prises en compte.
Ces limitations découlent des hypothèses simplificatrices qui ont été faites lors de sa dérivation et des conditions de validité qui s’appliquent à son utilisation.
Hypothèses simplificatrices et conditions de validité
L’équation de chasse d’eau est basée sur un certain nombre d’hypothèses simplificatrices, notamment :
- L’écoulement est considéré comme étant incompressible et non visqueux. Cela signifie que la densité du fluide est constante et que les forces de frottement sont négligées. Cette hypothèse est valable pour la plupart des applications d’évacuation, mais elle peut devenir moins précise pour les écoulements à haute vitesse ou dans les tuyaux étroits.
- L’écoulement est supposé être unidimensionnel. Cela signifie que la vitesse du fluide est constante sur toute la section transversale du tuyau. Cette hypothèse est valable pour les tuyaux de grand diamètre, mais elle peut devenir moins précise pour les tuyaux de petit diamètre où l’écoulement peut devenir turbulent.
- L’équation de chasse d’eau suppose que le niveau d’eau dans le réservoir est constant. Cette hypothèse est valable pour les réservoirs de grande capacité, mais elle peut devenir moins précise pour les réservoirs de petite capacité où le niveau d’eau peut varier considérablement pendant la chasse d’eau.
Cas où l’équation peut ne pas être précise
L’équation de chasse d’eau peut ne pas être précise dans les cas suivants :
- Écoulements turbulents : L’équation de chasse d’eau est basée sur l’hypothèse d’un écoulement laminaire, qui est caractérisé par un mouvement fluide et ordonné. En réalité, les écoulements dans les systèmes d’évacuation sont souvent turbulents, ce qui signifie que le fluide se déplace de manière chaotique et irrégulière.
The Chasse d’Eau equation, a cornerstone of hydraulics, calculates the discharge rate of water through an orifice. It’s a fundamental principle in understanding fluid flow, just as choosing the right housse de couette fille is crucial for a comfortable sleep.
The Chasse d’Eau equation finds applications in various engineering fields, including water management and irrigation systems.
La turbulence peut entraîner des pertes de charge importantes qui ne sont pas prises en compte par l’équation de chasse d’eau.
- Changements de section transversale du tuyau : L’équation de chasse d’eau suppose que la section transversale du tuyau est constante. Cependant, dans les systèmes d’évacuation, il est courant de rencontrer des changements de section transversale, tels que des coudes, des raccords et des rétrécissements.
Ces changements peuvent affecter la vitesse et la pression du fluide, ce qui peut rendre l’équation de chasse d’eau imprécise.
- Pertes de charge importantes : L’équation de chasse d’eau ne tient pas compte des pertes de charge dues au frottement du fluide sur les parois du tuyau, aux coudes et aux raccords. Ces pertes de charge peuvent être importantes, en particulier pour les écoulements à haute vitesse ou dans les tuyaux de grand diamètre.
Méthodes alternatives pour analyser les systèmes d’évacuation
Dans les cas où l’équation de chasse d’eau n’est pas précise, il existe des méthodes alternatives pour analyser les systèmes d’évacuation. Ces méthodes comprennent :
- Modélisation numérique : La modélisation numérique utilise des logiciels informatiques pour simuler le comportement des systèmes d’évacuation en tenant compte des effets de la turbulence, des changements de section transversale et des pertes de charge. Cette approche est plus complexe que l’équation de chasse d’eau, mais elle peut fournir des résultats plus précis.
- Essais expérimentaux : Les essais expérimentaux impliquent la construction d’un modèle physique du système d’évacuation et la réalisation de tests pour mesurer le débit, la vitesse et la pression du fluide. Cette approche est coûteuse et prend du temps, mais elle peut fournir des données précises pour valider les modèles numériques.
Études de cas et exemples: Chasse Deau Equation
L’équation de chasse d’eau trouve des applications pratiques dans divers domaines, notamment la conception de systèmes d’égouts, la gestion des eaux usées et l’optimisation des systèmes de drainage. Les études de cas suivantes illustrent l’utilisation de l’équation de chasse d’eau dans des scénarios réels et mettent en évidence les défis rencontrés et les solutions adoptées.
Exemples d’applications de l’équation de chasse d’eau
L’équation de chasse d’eau est un outil précieux pour comprendre et prédire le comportement du flux d’eau dans les systèmes de drainage et d’égouts. Voici quelques exemples concrets d’applications de l’équation de chasse d’eau dans des études de cas réelles:
| Étude de cas | Objectif | Méthodologie | Résultats |
|---|---|---|---|
| Optimisation d’un système de drainage urbain | Réduire les inondations et améliorer l’efficacité du drainage | Utilisation de l’équation de chasse d’eau pour simuler le débit d’eau dans les canaux de drainage et identifier les points d’étranglement | Amélioration du système de drainage, réduction des inondations et augmentation de la capacité de drainage |
| Conception d’un réseau d’égouts pour une nouvelle ville | Déterminer la taille optimale des tuyaux d’égouts et la capacité du système | Application de l’équation de chasse d’eau pour calculer les débits d’eaux usées et dimensionner les tuyaux en conséquence | Conception d’un réseau d’égouts efficace et durable, minimisant les coûts de construction et d’entretien |
| Évaluation de l’impact des précipitations sur un système d’égouts | Prédire la capacité du système d’égouts à gérer les événements pluvieux intenses | Utilisation de l’équation de chasse d’eau pour simuler le débit d’eau dans le système d’égouts pendant les événements pluvieux | Identification des points faibles du système et des mesures à prendre pour améliorer sa résistance aux fortes précipitations |
Défis et solutions
L’application de l’équation de chasse d’eau dans des études de cas réelles peut présenter des défis, notamment:
- La complexité du système d’égouts et la présence de nombreux facteurs influents.
- La disponibilité des données précises sur les débits d’eau, les caractéristiques des tuyaux et les conditions de terrain.
- La nécessité de prendre en compte les variations saisonnières des débits d’eau et les événements pluvieux extrêmes.
Pour relever ces défis, les ingénieurs peuvent adopter les solutions suivantes:
- Simplifier le modèle du système d’égouts en utilisant des approximations et des hypothèses réalistes.
- Recueillir des données précises sur les débits d’eau, les caractéristiques des tuyaux et les conditions de terrain.
- Utiliser des logiciels de simulation avancés pour prendre en compte les variations saisonnières et les événements pluvieux extrêmes.
L’équation de chasse d’eau est un outil puissant pour comprendre et prédire le comportement du flux d’eau dans les systèmes de drainage et d’égouts. Cependant, il est important de noter que l’équation est une simplification de la réalité et qu’il est essentiel de prendre en compte les limitations de l’équation lors de son application dans des études de cas réelles.
Tendances futures et innovations
L’équation de chasse d’eau, bien qu’elle soit un outil précieux pour comprendre et analyser le comportement des systèmes d’évacuation, est susceptible d’être encore améliorée et étendue grâce aux progrès technologiques. L’intégration de la modélisation numérique et des techniques d’apprentissage automatique ouvre de nouvelles possibilités pour une analyse plus précise et efficace des systèmes d’évacuation.
Modélisation numérique et apprentissage automatique
L’utilisation de la modélisation numérique et des techniques d’apprentissage automatique représente une avancée majeure dans le domaine de l’analyse des systèmes d’évacuation. Ces méthodes permettent de simuler le comportement complexe des écoulements d’eau et de prédire l’impact des variations des paramètres du système, tels que la géométrie des conduits, la pression d’alimentation et la viscosité du fluide.
La modélisation numérique permet de créer des modèles virtuels des systèmes d’évacuation, offrant une meilleure compréhension des phénomènes physiques en jeu.
- La modélisation numérique permet de simuler le comportement des systèmes d’évacuation en tenant compte de facteurs complexes tels que la turbulence, la friction et les effets de gravité. Elle permet de prédire avec précision le temps de vidange, la vitesse de l’écoulement et la pression dans le système.
- Les techniques d’apprentissage automatique peuvent être utilisées pour analyser de grandes quantités de données provenant de simulations numériques ou de mesures expérimentales. Ces algorithmes permettent d’identifier des tendances et des corrélations complexes, permettant d’améliorer la précision des prédictions et de développer des modèles plus robustes.
Innovations potentielles
Les tendances futures dans le domaine de l’analyse des systèmes d’évacuation conduisent à des innovations potentielles qui pourraient améliorer la précision et l’efficacité de l’équation de chasse d’eau.
- Le développement de modèles numériques plus précis et plus sophistiqués, intégrant des facteurs complexes tels que la cavitation et la turbulence, permettra de mieux prédire le comportement des systèmes d’évacuation dans des conditions réelles.
- L’intégration de capteurs intelligents dans les systèmes d’évacuation permettra de collecter des données en temps réel sur les paramètres du système, telles que la pression, la température et le débit. Ces données peuvent être utilisées pour améliorer la précision des modèles numériques et pour développer des systèmes de surveillance et de contrôle plus efficaces.
- L’utilisation de techniques d’apprentissage automatique pour optimiser la conception des systèmes d’évacuation permettra de réduire la consommation d’eau et d’énergie, tout en améliorant les performances du système.
L’équation de chasse d’eau est un outil précieux pour les ingénieurs et les concepteurs qui travaillent avec les systèmes d’évacuation. En comprenant ses principes et ses limitations, on peut l’utiliser efficacement pour optimiser les performances des systèmes d’évacuation et garantir leur fiabilité.
Expert Answers
Comment l’équation de chasse d’eau est-elle utilisée dans la conception des systèmes d’évacuation ?
L’équation de chasse d’eau permet de déterminer les dimensions optimales des tuyaux et les débits d’eau nécessaires pour assurer un écoulement efficace et prévenir les problèmes de refoulement.
Quelles sont les principales limitations de l’équation de chasse d’eau ?
L’équation est basée sur des hypothèses simplificatrices et peut ne pas être précise dans des conditions complexes, telles que les écoulements turbulents ou les changements brusques de section transversale du tuyau.
Quelles sont les tendances futures dans le domaine de l’analyse des systèmes d’évacuation ?
L’utilisation de la modélisation numérique et des techniques d’apprentissage automatique est en plein essor, offrant des possibilités d’améliorer la précision et l’efficacité de l’analyse des systèmes d’évacuation.